Arithmetic Border for a Square
This problem is from Grant Fikes.
Fill in integers in the table below so that each row and each column of the border of the square is an arithmetic sequence. Note: The incremental change may be different for each of the four sequences.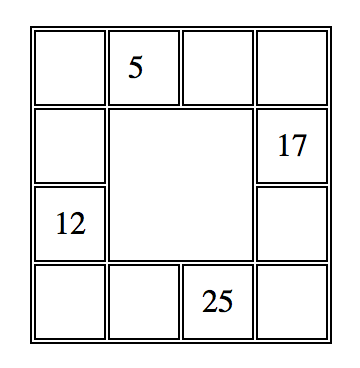
Submit your answers to mathpotw@acu.edu. Details for submissions can be found here.
Solution to Arithmetic Border for a Square
Correct solutions were submitted by: Brookley Baker, Wyatt Witemeyer, Lauren Ferraro, Jared Mayfield, Jared Barker, Bethany Witemeyer
Let x be the unknown value of the northwest corner of the table. Using the fact that an arithmetic sequence has a constant difference between terms, we can fill in the rest of the unknown slots in terms of x. Here is the result:
| x | 5 | 10 – x | 15 – 2x |
| 8x – 9 | 17 | ||
| 12 | 19 + 2x | ||
| 25 – 8x | 33 – 4x | 25 | 21 + 4x |
We can now get an equation involving x using the top three cells in the left column of the table. Namely:
(8x – 9) + ((8x – 9) – x) = 12.The solution of this equation is x = 2. Therefore the filled-in table is:
| 2 | 5 | 8 | 11 |
| 7 | 17 | ||
| 12 | 23 | ||
| 17 | 21 | 25 | 29 |

